(a)
(b)
SELECTED PROBLEMS
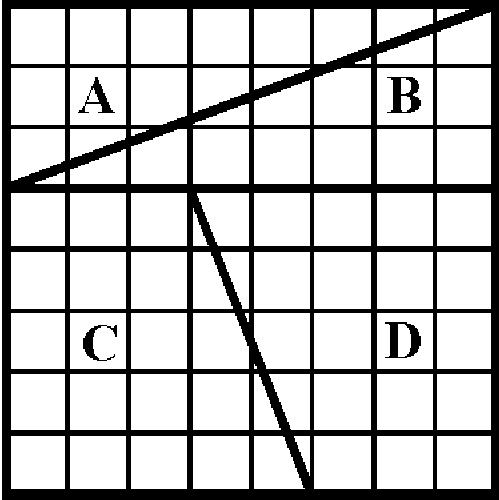
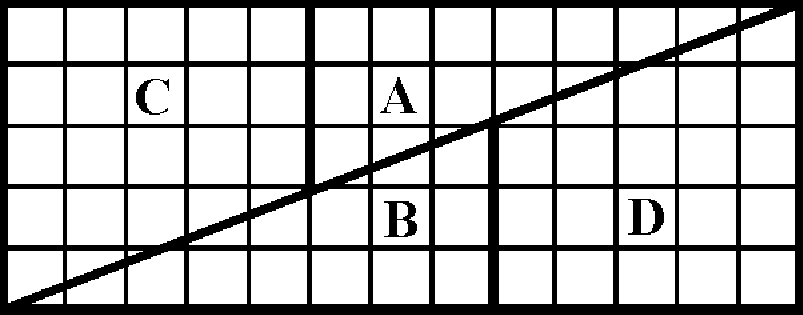
1. GEOMETRICAL PARADOX: 64=65.
The chessboard is divided into four pieces---A, B, C, and D, as shown in figure a. If these four pieces are put together in the shape of a rectangle, as shown in figure b, one obtains a 5x13 rectangle containing 65 small squares. Therefore, 64=65?! Can you explain this phenomenon? Geometrical fallacy: 64 = 65?
|
|
|
|
|
(a) |
(b) |
|
Solution: The paradox arises from the fact that the edges of the four pieces A, B, C, and D, which lie along the diagonal of the formed rectangle, do not coincide exactly in direction. This diagonal is not a straight segment line but a small lozenge (diamond-shaped figure), whose acute angle is
arctan 2/3 - arctan 3/8 = arctan 1/46
which is less than 1° 15' . Only a very precise drawing can enable us to distinguish such a small angle. Using analytic geometry or trigonometry, we can easily prove that the area of the "hidden" lozenge is equal to that of a small square of the chessboard.
|
2. CYLINDRICAL CHESS. The pieces in so-called cylindrical chess are arranged as on the ordinary chessboard, and they move following the same rules. But the board is in a cylindrical form because its vertical edges are joined ("vertical cylindrical chess") so that the verticals a and h are juxtaposed. M. S. Petkovic posed the problems regarding vertical cylindrical chess (figure). How can White play and mate in his second move at latest, against any black defence? Solution: The first White move is 1. Nh4-b5!!. After 1... K:b5 White plays along the fouth horizontal and mates by 2. Qg4-a4 using the support of the pawn. If 1... Kd5 then 2. Qe6 mate. (N - Knight; Q - Queen, K - King). |
|
[
More problems][
About Miodrag Petkovic] [Mathematics and Chess]